6.9.5 Rocking SpheresThe following example demonstrates how to create accelerations by using "cos()" function in a formula. 1. Create two spheres, one white and one black. 2. Add the following tags to the spheres: White sphere: SFOR x=t*0.5+(t)*(0.5+0.5*cos(8*PI*t)) 3. Create a SIMPLE SKELETON method to the same level with the spheres. 4. Create a B-Spline curve under the method level as shown in the picture below. |
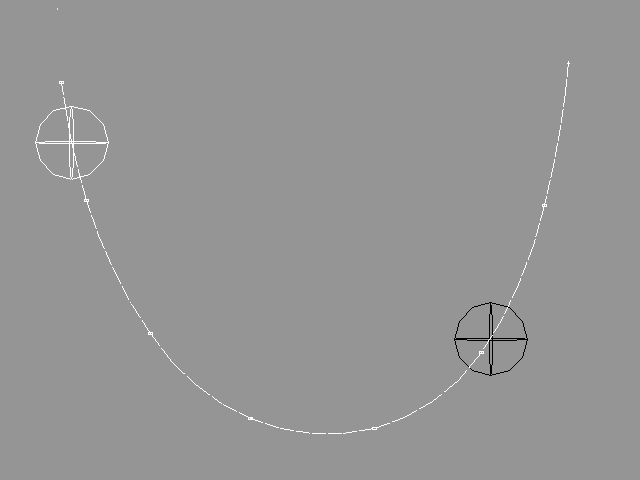 YouTube Figure T6-29: Spheres Rocking along a Skeleton Curve. |
|
Play the animation and the spheres will behave in a very natural way. Lets analyze the formulas we attached to the target objects. The time (t) goes from 0 to 1 in our example when the animation is played. Thus, in the beginning, the first part of the formula, "t*0.5", has no effect at all. When the animation proceeds, the term "t*0.5" approaches 0.5. On the other hand, the rest of the formula "(1-t)*(0.5+0.5*cos(8*PI*t))" gets weaker and weaker because "(1-t)" approaches 0. So, in the beginning, the function "cos()" causes the sphere to roll up and down in its full power but in the end, it does not affect the position of the sphere at all. If math is not one of your strong points, don't worry, there will be lot of nice ready-made formulas available very soon! |
| ghh don'tpanic |